統計学の本でベイズは何回か出てきたが、なかなか自分の中で理解しきれなくて頭の中に残っておらず、ベイズに関しての本を読み直し、もう少し自分の中で消化することにしてみた。今後、ベイズを使った最適化などを検討するケースもあるので、簡単な実装ができるようにするため、まずは初歩的なところを整理してみる。
ベイズの定理
ベイスの定理は一見難しいけど、実は当たり前の計算式になっている。下の式は、XとYの両方の事象が起きるときの確率は、Yが起きたときにXが起きるときの確率と、その逆のXが起きたときにYが起きる確率とで同じになる。
$${P(X|Y)}{P(Y)} = {P(Y|X)}{P(X)}$$
これを少し変形するとベイズの定理の式になる。
$$P(X|Y) = \frac{{P(Y|X)}{P(X)}}{P(Y)} = \frac{{P(Y|X)}{P(X)}}{{P(Y|X)}{P(X)} + {P(Y|\bar X)}{P(\bar X)}}$$
例として、1000人に1人が罹患している病気Xの検査で、陽性反応が出てしまった場合の実際に罹患している確率を計算してみる。罹患の確率は1000人に1人なので\(P(X)=0.001\) 。これまでの調査結果から、罹患している人が検査で陽性になる確率は90%(10%は陰性の結果が出る)で、罹患してない人でも5%は陽性の結果が出てしまうことがわかっている。(\(P(Y|X)=0.9\) で \(P(Y|\bar X)=0.05\) )
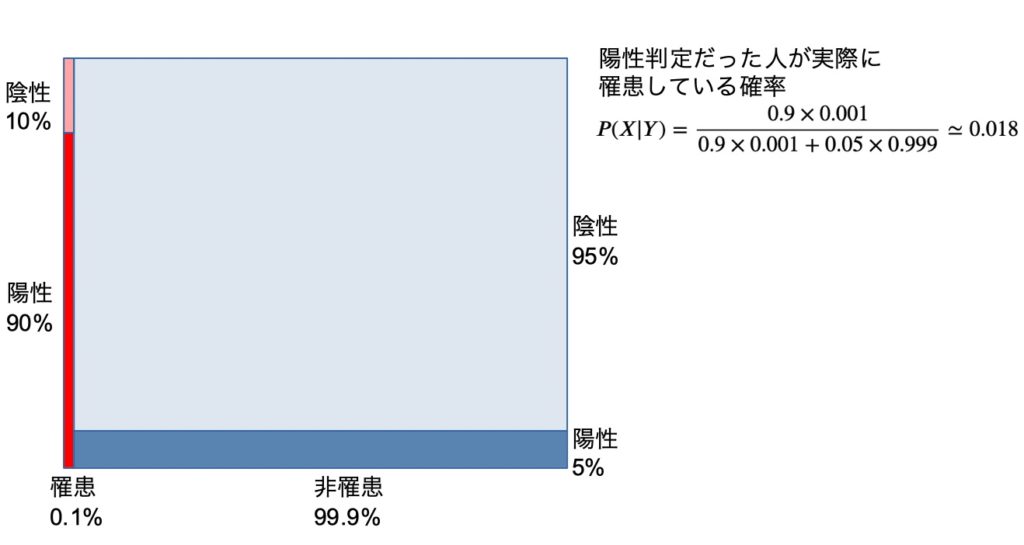
ベイズの定理に入れると陽性の結果を受けたとしても実際に罹患している確率は1.8%となり、心理的には検査が陽性だとほぼほぼ病気に罹っている気がしてしまうが、実際に罹患している確率は意外と低い。これは元々の罹患率が低いためである。
これは実際に罹患率が低くて安心するケースであるが、これを同じように工場の品質検査の例に当てはめてみる。罹患=不良品、非罹患=良品として、陽性=NG判定、陰性=OK判定とすると、検査での再現率は90%とかなり高いが、現場ではNG判定品が本当に不良なのは1.8%程度で、実際にはほとんど良品ということになる。かなりいい精度の判定モデルでも、現場ではほとんどが誤判定ということになる。
ここで求めるのに使った罹患率\(P(X)\)を事前確率、罹患している人が実際に陽性である確率\(P(Y|X)\)を尤度、求めた答えの\(P(X|Y)\)を事後確率という。
また、通常では、原因から結果を推測するが、ベイズの場合は逆で結果(陽性)を元に原因(罹患)を推測する逆順序になっているのがベイズの特徴。
ベイズ更新
上の病気の例では事前確率である罹患率が0.1%とわかっていたが、実際には事前確率が判明していないケースもある。そのようなケースでは、主観的に考えられる確率を使い、得られた事後分布を事前確率として使うことで、精度をあげていくことができ、これをベイズ更新と言う。
例えば、釣り船でタイ釣りに行ったとする。エリアAからDまであって、どこに行けばタイをいっぱい釣れるかを考えてみる。事象Xはタイがいる確率\(p_i\)、事象Yは実際にタイが釣れる確率\(q_i\)。過去の経験から主観的であるが、今日の天気、潮の流れなどから、4つのエリアでタイがいる確率、釣れる確率が下記の表のようにそれぞれ経験的にわかっている。(\(_i\)はAからDが入る)
| A | B | C | D | 計 | |
| タイがいる確率\(P(X)=p_i\) | 0.3 | 0.4 | 0.2 | 0.1 | 1.0 |
| タイがいない確率\(P(\bar X)=1-p_i\) | 0.7 | 0.6 | 0.8 | 0.9 | – |
| タイが釣れる確率\(P(Y)=q_i\) | 0.4 | 0.5 | 0.3 | 0.2 | – |
| タイが釣れない確率\(P(\bar Y)=1-q_i\) | 0.6 | 0.5 | 0.7 | 0.8 | – |
あるエリアに行って、タイが釣れなかった場合\(P(\bar Y)\)で、実はそこにタイがいた事後確率を\(pi’\)とすると、ベイズの定理は以下のように変形される。(分母の\(P(\bar Y|\bar X)=1\)とみなす。魚がいないエリアでは釣れないため)
$$p’_i=P(X|\bar Y)= \frac{{P(\bar Y|X)}{P(X)}}{P(\bar Y)}= \frac{{P(\bar Y|X)}{P(X)}}{{P(\bar Y|X)}{P(X)} + {P(\bar Y|\bar X)}{P(\bar X)}} = \frac{p(1-q)}{1-pq}$$
上の表から最初はエリアBが一番タイがいる確率が高いので、エリアBを選択して釣りをするが、ここで釣れなかったとする。釣れなかった場合の事後確率\(p’_B\)を計算し、次のアクションの事前確率となる。他の3つのエリアの事前確率は、\(p’_B\)を除いて比例配分する。これを繰り返した結果が以下になる。
| A | B | C | D | 計 | 釣り場 | |
| 初期値 | 0.3 | 0.4 | 0.2 | 0.1 | 1.0 | B |
| 1回目の釣り場 | 0.375 | 0.250 | 0.250 | 0.125 | 1.0 | A |
| 2回目の釣り場 | 0.256 | 0.298 | 0.298 | 0.149 | 1.0 | C |
| 3回目の釣り場 | 0.283 | 0.330 | 0.222 | 0.165 | 1.0 | B |
学んで感じたこと
このように主観的な数字で正確な分布がわかってなくても、直感を元に得られた結果から更新して原因の確率を予測するのがベイズで、人の感覚に近い。一方で最初の罹患率の例のように、人の感じる物事の重大さ(陽性反応)と実際の罹患率との乖離が大きく、人の感じることはFactと異なる。ここは感情的な面や不安な要素に強く反応する人の脳の特性とかも関係している?
ベイズ統計は主観的な確率を用いることに対しての批判があり、ずっと日の目が当たらなかったという歴史があったが、最近では迷惑メールフィルターや、病気の因果関係を探るなど応用範囲が広がっている。ここから最適化に応用するところを次のステップでやっていきたい。
参考文献
Python コンピュータシミュレーション(オーム社)
https://www.ohmsha.co.jp/book/9784274226984/