娘が小学校でもらってきたツタンカーメンえんどう豆の栽培を始めて2年目になる。ちょうど今の季節、以下の写真のように紫色のさやの実がなっていて、緑色のさやもある。えんどう豆といえば、メンデルの法則、ちょうど先月から生命科学について勉強し始めていて、ゲノムとセントラルドグマによる遺伝子発現の続きとして、今回はちょうど勉強したばかりの遺伝子について、庭で栽培したえんどう豆の遺伝で考えてみる。

メンデルの法則
遺伝を最初に法則としてまとめたのは生物の授業でも出てくるメンデル。エンドウ豆で種子の形や色、花の色など7つの対立する形質を交配実験して、3つの法則(優性、分離、独立)を1866年に発表した。
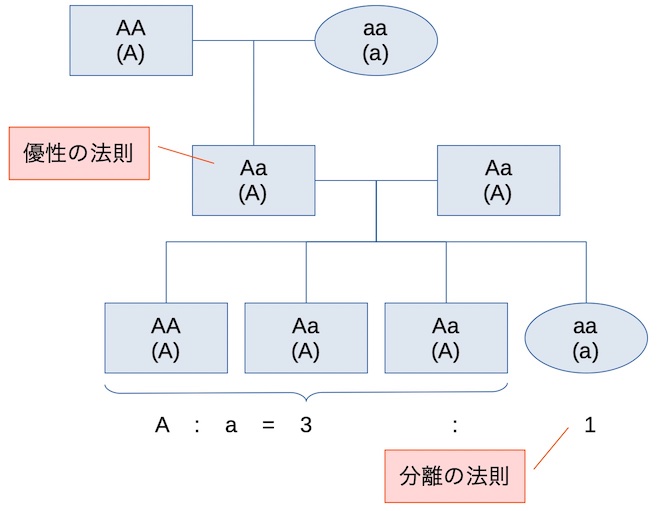
優性の法則は、形質に優劣があり、仮に親から対立する両方の遺伝子を引き継いだとしても優性の遺伝子があると、劣勢の方は現れてこないという法則。両親の片方が遺伝子をAAを持ち、もう片方が aaを持つ時、子世代(F1)は全てAaとなるが、Aがaより優性だと子はみんなAの形質を現すようになる。ツタンカーメンえんどう豆だと紫色のさやが多くて優性であるようだ。
分離の法則は、Aaの子同志が交配する孫世代(F2)と、aaを有してaの形質を現すものが出てくるという法則。これはAaが分離されて別々の配偶子に入るためである。
最後の独立の法則は、Aとa以外に、Bとbという別の形質を現す遺伝子があった場合、Aとa、Bとbは全く独立で影響されることなく遺伝するという法則。
ハーディー・ワインベルク平衡
対立遺伝子Aとaの確率が\(p\)と\(q\)(=1-\(p\))だとする。その場合、各遺伝子頻度は、AAは\(p^2\)、Aaは\(2pq\)、aaは\(q^2\)に一致するという法則。この法則が当てはまるには集団のサイズが十分大きい、交配がランダム、突然変異が生じない、他集団へ移住しないなどの条件である。要は外からのノイズがなくて、突然変化もないのであれば、数式で計算できる値で平衡するということになる。
今年のうちのプランター栽培では、紫色が16株、緑色が9株だった。紫色のさやの遺伝子がA、緑色のさやの遺伝子がaとし、Aが優性遺伝子とする。AA = 5、Aa = 11、aa = 9と仮定してみると、集団のサイズが全然大きくないが、以下の図のように期待値を出してカイ2乗で検定すると、平衡が成り立つ。AAとAaの個体数は実際に調べることは個人ではできないため、あくまで仮定上の数字。そもそも集団サイズが小さく、この法則が当てはまる条件にも合致してないため、この計算が正しいかどうはあるが、Aの確率は\(p\)=0.42に近いのでないかと推測している。

遺伝子浮動
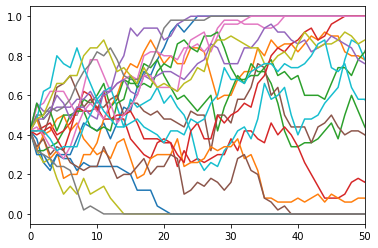
これが世代でどのように遺伝子頻度が変わるのかをシミュレーションしてみる。紫色と緑色とで絶対的な優位がないとすると、どちらとも自然淘汰されずに、「偶然により」対立遺伝子の頻度が変わってくる。これを遺伝子浮動と言う。シミュレーション結果がしたのグラフだが、横軸は世代数、縦軸は遺伝子頻度で’1’が紫色、’0’が緑色になる。波形が重なっているのは、ランダムにシミュレーションを20回実行した結果を重ね書きしている。遺伝子頻度の初期値を上のハーディ・ワインベルグでの値を使ったとしても、次の世代ではランダムに遺伝子頻度が変わり、最終的に全てが紫色になったり、緑色になったりする。
遺伝子の自然選択
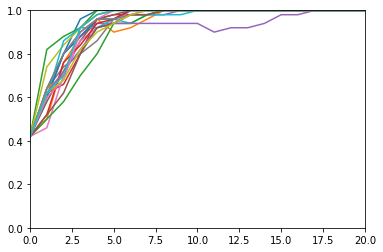
ダーウィンの進化論では、生存競争に有利なものは保存され、有利でないものは除去される。このことを自然選択とか自然淘汰と呼ぶ。この自然選択ではないけど、緑色のさやだけを食べてしまって、紫色のさやは種として残すとする。緑色の遺伝子は食べてしまうため、各世代ともに半減してしまうと仮定してシミュレーションをしてみると以下の結果になる。大体3~4世代ぐらいになるとほぼほぼ紫だけになる。
えんどう豆は自家受粉なので、AAはAAと、AaはAaと、aaはaaと受粉することになる。上記のようにランダムにはいかないと思われ、メンデルの法則だとAaが残る限りはaaの緑色が出続けることになるが、今後数年間、観測を続けてみたい。
ちなみにうちのえんどう豆を観察していると、アブラムシが多くついているのは緑色のさやに多いように感じる。紫色の方はそういった意味では生き残りやすいのかもしれない。
参考記事
遺伝子浮動の計算は以下のコードを参照。
http://www.biology.kyushu-u.ac.jp/~kteshima/Information/20170802_simulation_with_random_number.html