今まで仕事でも教師あり学習や教師なし学習などを取り扱うケースは多かったが、機械学習のもう一つの手法の強化学習についてあまり触れたことがなかったので整理してみた。ある行動を起こして、それに対しての結果からの報酬や価値を最大化する形で学習していく手法で、将棋AIや囲碁AI、自動運転とかで使われている。子供が自転車でこけたり、うまくいったことを経験しながらだんだんと自転車が乗れるようになっていくようなイメージで、人の学習プロセスに近い。わかりやすい本(つくりながら学ぶ!深層強化学習:小川雄太郎著:マイナビ出版)があったので、それをもとに実際に試してみる。
基本用語の整理
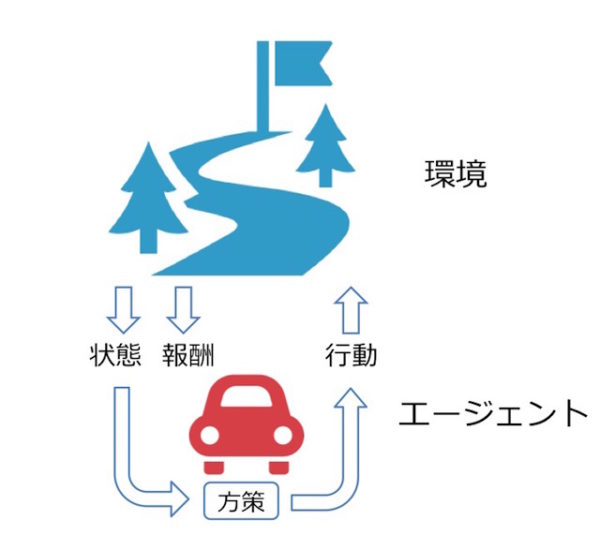
強化学習を学ぶ中で、言葉の定義がわかったつもりで、段々と混乱してきたので、図で整理してみる。ある環境の中で、行動を起こすエージェントがいる。エージェントは方策をもとに行動を起こすことによって、状態と報酬がFeedbackされ、それをもとに方策を更新する。
この図の中には価値がないが、強化学習では価値を最大化させる必要がある。報酬と価値の違いは、報酬はある行動に対しての報酬であり、価値は一連の行動を通じて得られる効用。
強化学習の目的は価値を最大化させる最適な方策を作り出すことになる。
強化学習の手法
強化学習には大きく2つの手法があり、方策反復法と価値反復法がある。方策反復法は最後のゴールまで実行し、ゴールまでのステップ数を評価し、そこでの有効な行動を学習していく方法。価値反復法はゴールから逆算して、ゴールまでの途中経過にも価値を与えて、価値を最大化する行動を獲得していく方法。
方策反復法
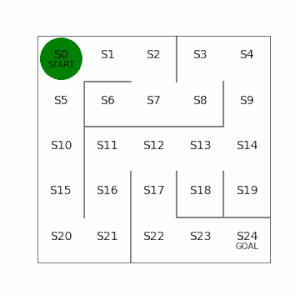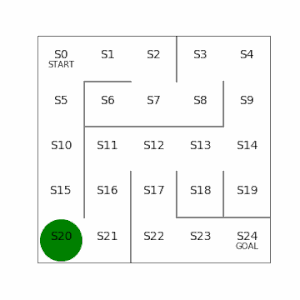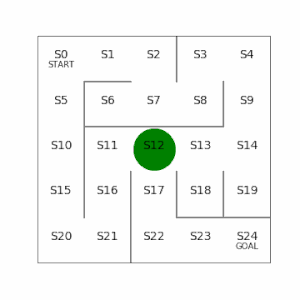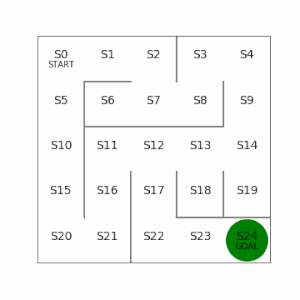
方策反復法は、最後のゴールまで行動し、ステップ数が少ないものが最適解に近いとして学習の重みを大きくする。勾配法を使っていて収束してきたら学習を打ち切る。実装は本のコードのとおり。ただし、本では3×3の迷路だったが、もう少し複雑にして5×5と6×6で試してみる。
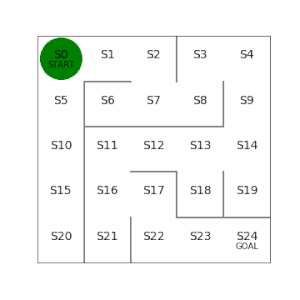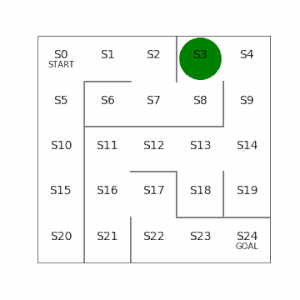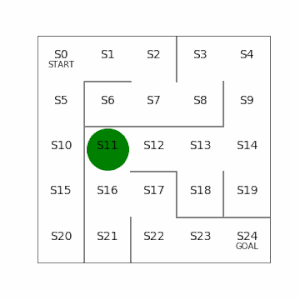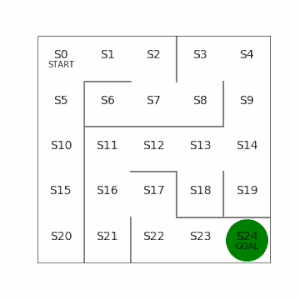
左側が学習した結果。ゴールまでのステップ数は16で、最短でたどり着く形で学習できている。
右側は迷路の左下を少しいじってみて、ゴールまでの経路が2つあるように変更。左側の経路を通った方がステップ数が12と最短でいけるが、この最短経路もしっかり学習で見つけることができている。
ちなみに左側のケースで、学習終了までの回数は55476回、時間はMacbook Air(2013)で218sec。
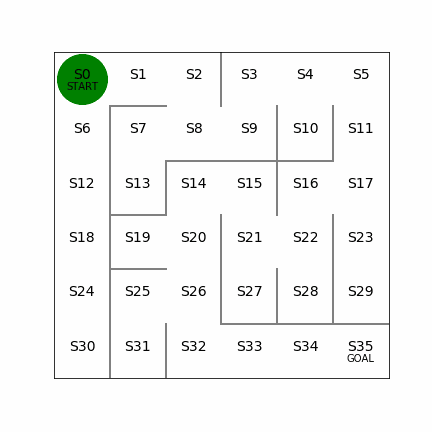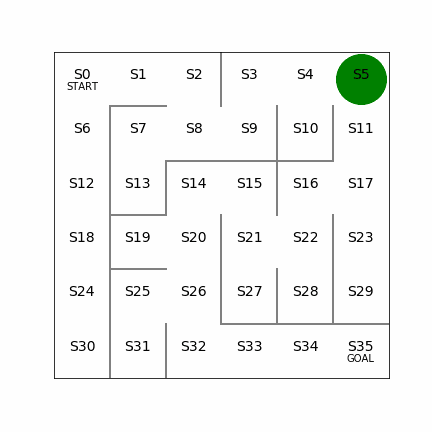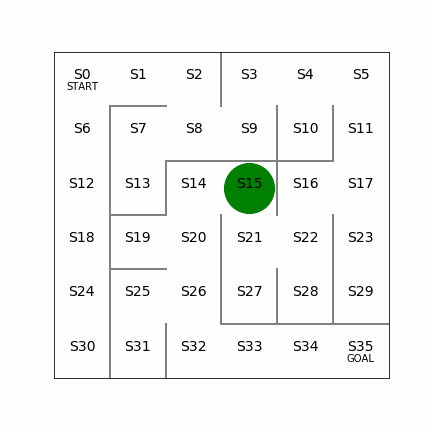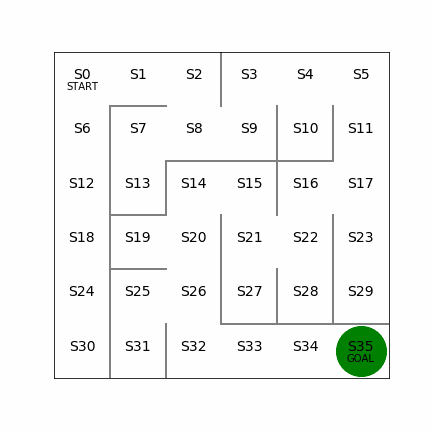
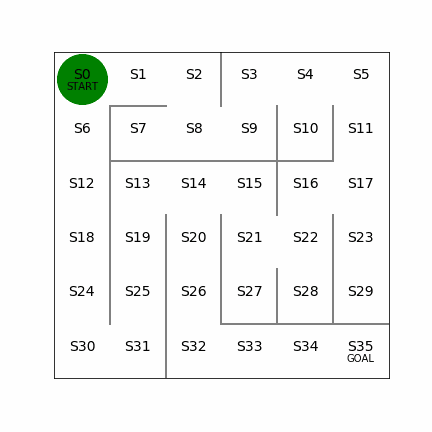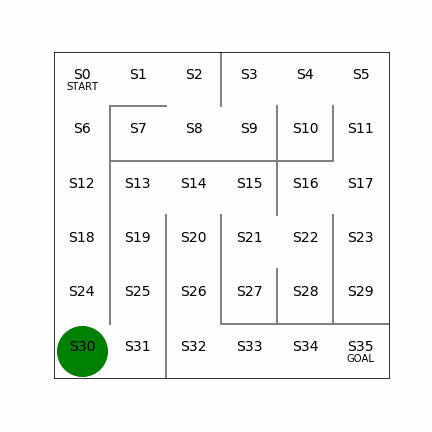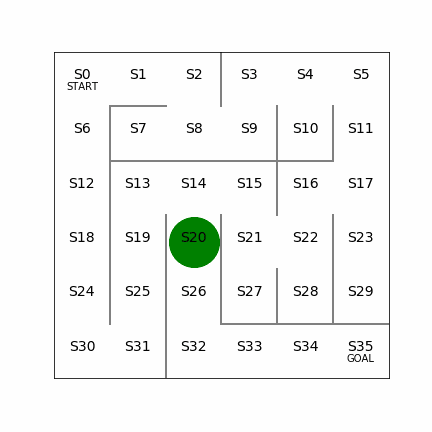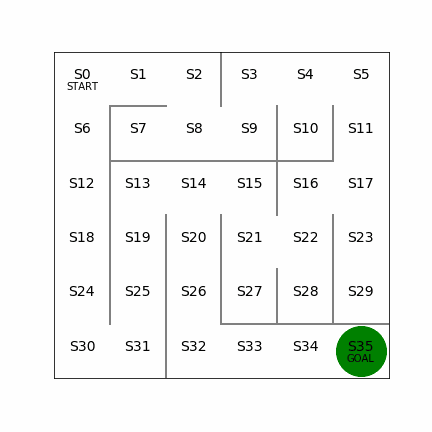
次の迷路をXY方向ともに一つずつ増やして、6×6にしてみる。同じく左側では20回でゴールまでたどり着くケース。右側は迷路の左側を変えてみて、こちらも経路が2つできる形になるが、左側の経路を使うと16回でゴールまでたどり着くことができる。こちらもしっかりと最短経路を見つけることができている。これぐらいの規模だと局所解になるようなことはないのかもしれない。
6×6の場合の学習回数は87595回、学習に要した時間は417sec。
価値反復法
価値反復法では2つの価値、行動価値と状態価値を定義する。ここのところの理解がかなり難しいが、このページの一番上の図を頭の中にイメージしたら少しはわかりやすくなるのかもしれない。
行動価値:言葉のとおり、ある状態(s)で取った行動(a)によって、得られる報酬の価値。例えば5×5でS23にいて、右側に行く行動をとると報酬がもらえるが、左側に行く行動をとると遠ざかる分だけ報酬の価値が割り引かれる。
状態価値:ある状態(s)自体の価値。具体的には、状態(s)で方策(π)に従って行動することで将来的に期待される割引込みの報酬和。
価値反復法では方策反復法と違い、状態を遷移するステップごとに行動価値を更新する。そしてゴールまでの一連の行動(エピソード)を通じて状態価値を更新、この状態価値を最大化していくことになる。このとき、たまたま価値が大きくなった場合にその経験に強く影響されてしまい、局所解に陥る可能性がある。そのため、ε-greedy法と呼ばれる方法で、一定の確率εでランダムに行動するようにする。
行動価値の求め方の違いによって、SarsaやQ学習のアルゴリズムが変わってくる。以下はQ学習での5×5迷路で、300回(エピソード)学習した結果。状態価値が毎エピソードを通じてどのように変わっていくかをヒートマップで示している。方策反復法と違って学習時間はかなり短い。

まとめ
強化学習の最初の一歩的な知識をまとめてみた。これだけでも理解するのにかなり時間を要したが、本を読むだけだと頭に残らないのと、理解したつもりで理解できてないことが多いので、まとめることで自分の頭の中が整理できたと思う。時間ができたら、深層強化学習まで深堀したいのと、強化学習の課題、「失敗が許されない環境の中では実験が行いにくい」という課題に対して、バーチャルな環境の構築方法をもう少しイメージできるようにしていきたい。